算法总结

发表于 更新于 分类于 阅读次数： Changyan： 本文字数： 11k 阅读时长 ≈ 19 分钟

思想

大部分算法可以看作对于二叉树的操作

二叉树解题的思维模式分两类：

1、是否可以通过遍历一遍二叉树得到答案 ？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案 ？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论使用哪种思维模式，你都需要思考：

如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做 ？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

  • 比如快排是二叉树前序遍历
1
2
3
4
5
6
7
8
9
void sort(int[] nums, int lo, int hi) {
    /****** 前序遍历位置 ******/
    // 通过交换元素构建分界点 p
    int p = partition(nums, lo, hi);
    /************************/

    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}
  • 归并排序是二叉树后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
void sort(int[] nums, int lo, int hi) {
    int mid = (lo + hi) / 2;
    // 排序 nums[lo..mid]
    sort(nums, lo, mid);
    // 排序 nums[mid+1..hi]
    sort(nums, mid + 1, hi);

    /****** 后序位置 ******/
    // 合并 nums[lo..mid] 和 nums[mid+1..hi]
    merge(nums, lo, mid, hi);
    /*********************/
}

前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点

  1. 前序位置的代码在刚刚进入一个二叉树节点的时候执行；
  2. 后序位置的代码在将要离开一个二叉树节点的时候执行；
  3. 中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

两大框架

回溯框架【遍历】

DFS

DFS 的关注点在单个 节点

1
2
3
4
5
6
7
8
9
10
11
// DFS 算法把「做选择」「撤销选择」的逻辑放在 for 循环外面
void dfs(Node root) {
    if (root == null) return;
    // 做选择
    print("我已经进入节点 %s 啦", root)
    for (Node child : root.children) {
        dfs(child);
    }
    // 撤销选择
    print("我将要离开节点 %s 啦", root)
}

回溯

回溯算法的关注点在节点间的 树枝

1
2
3
4
5
6
7
8
9
10
11
// 回溯算法把「做选择」「撤销选择」的逻辑放在 for 循环里面
void backtrack(Node root) {
    if (root == null) return;
    for (Node child : root.children) {
        // 做选择
        print("我站在节点 %s 到节点 %s 的树枝上", root, child)
        backtrack(child);
        // 撤销选择
        print("我将要离开节点 %s 到节点 %s 的树枝上", child, root)
    }
}

站在一个节点上我们需要考虑三个问题：

  1. 路径：也就是已经做出的选择。

  2. 选择列表：也就是你当前可以做的选择。

  3. 结束条件：也就是到达决策树底层，无法再做选择的条件。

排列组合

分为三种情况：

  1. 元素无重不可复选 (基础)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    const backtrack = (start) => {
           // 前序遍历位置，每个节点的值都是一个子集
           result.push([...onPath]);
           
           // 回溯算法 --- 组合
           for (let i = start; i < nums.length; i++) {
               onPath.push(nums[i]);
               backtrack(i + 1);// 回溯遍历下一层节点
               onPath.pop();
           }
       };
    • 不可复选，则start代表从索引start开始选，无需考虑前面的因为已经选过了。

  2. 元素可重不可复选

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    nums.sort((a,b)=>a-b); //排序
    //... ...
    const backtrack = (start=0) => {
            // 前序遍历位置，每个节点的值都是一个子集
            result.push([...onPath]);
            
            // 回溯 --- 组合
            for (let i = start; i < nums.length; i++) {
                if(i>start && nums[i]==nums[i-1]) continue; //剪枝
                onPath.push(nums[i]);
                backtrack(i + 1);// 回溯遍历---从下一个元素开始
                onPath.pop();
            }
        };
    • 因为元素可重但是选择不可重，所以需要剪枝。
    • 先给nums排序，方便后面剪枝

  3. 元素无重可复选

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    nums.sort((a,b)=>a-b); //排序
    //... ...
    const backtrack = (start=0) => {
            // 前序遍历位置，每个节点的值都是一个子集
            result.push([...onPath]);
            
            // 回溯 --- 组合
            for (let i = start; i < nums.length; i++) {
                //剪枝
                onPath.push(nums[i]);
                backtrack(i);// 回溯遍历---从此元素开始
                onPath.pop();
            }
        };

BFS

层序遍历属于迭代遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
	let depth = 0;
    // 从上到下遍历二叉树的每一层
    while (!q.isEmpty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // 将下一层节点放入队列
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
        depth ++ ;
    }
}

变形递归

二叉当作三叉
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 三叉树遍历框架
function traverse(node1, node2) {
    if (node1 === null || node2 === null) {
        return;
    }
    /**** 前序位置 ****/
    // 将传入的两个节点穿起来
    node1.next = node2;
  
    // 连接相同父节点的两个子节点
    traverse(node1.left, node1.right);
    traverse(node2.left, node2.right);
    // 连接跨越父节点的两个子节点
    traverse(node1.right, node2.left);
}
从右向左的中序-倒序二叉搜索树
1
2
3
4
5
6
7
8
9
var traverse = function(root) {
    if (root == null) return;
    // 先递归遍历右子树
    traverse(root.right);
    // 中序遍历代码位置
    console.log(root.val);
    // 后递归遍历左子树
    traverse(root.left);
}

动规框架【分解】

1
2
3
4
5
6
# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):
    for 选择 in 所有可能的选择:
        # 此时的状态已经因为做了选择而改变
        result = 求最值(result, dp(状态1, 状态2, ...))
    return result
1
2
3
4
5
6
7
8
# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

动态规划问题必须符合 最优子结构

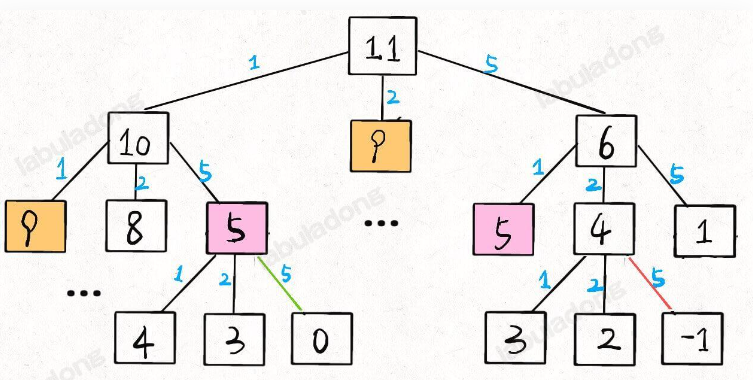
例如换零钱： 面值分别为 1，2，5，用最少硬币凑到总金额 amount = 11

子结构就是 凑到 10, 9, 6 的硬币数+12

子问题必须独立

因为每种硬币无限多，即凑到10元的结果，不影响凑到9元的结果

总结

对于动态规划的题目， 题目求什么，dp[i][j] 的值就代表什么。

DP树

DP树

压缩

如果计算状态 dp[i][j] 需要的都是 dp[i][j] 相邻的状态，那么就可以使用空间压缩技巧

链表

  • 双指针
  • 虚拟头节点: 需要创建新链表时

反转链表

递归方式

输入一个节点 head，将「以 head 为起点」的链表反转，并返回反转之后的头结点 。

1
2
3
4
5
6
7
8
9
ListNode reverse(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    ListNode last = reverse(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}

大根堆

求 n 个数字中的最大值

  • 由数组构成的完全二叉树
  • 两个功能: 插入和弹出
    • 插入: 插入队尾,队尾冒泡
    • 弹出: 队头和队尾交换,弹出队尾,队头下沉

    • 所有操作都在头尾

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
public class MaxPQ
    <Key extends Comparable<Key>> {
    // 存储元素的数组
    private Key[] pq;
    // 当前 Priority Queue 中的元素个数
    private int size = 0;

    public MaxPQ(int cap) {
        // 索引 0 不用，所以多分配一个空间
        pq = (Key[]) new Comparable[cap + 1];
    }

    /* 返回当前队列中最大元素 */
    public Key max() {
        return pq[1];
    }

    /* 插入元素 e
    要插入的元素添加到堆底的最后，然后让其上浮到正确位置。
 */
    public void insert(Key e) {...}

    /* 删除并返回当前队列中最大元素
    堆顶元素 A 和堆底最后的元素 B 对调，然后删除 A，最后让 B 下沉到正确位置。 */
    public Key delMax() {...}

    /* 上浮第 x 个元素，以维护最大堆性质 */
    private void swim(int x) {
        // 如果浮到堆顶，就不能再上浮了
        while (x > 1 && less(parent(x), x)) {
            // 如果第 x 个元素比上层大
            // 将 x 换上去
            swap(parent(x), x);
            x = parent(x);
        }
    }

    /* 下沉第 x 个元素，以维护最大堆性质 */
    private void sink(int x) {
        while (left(x) <= size) {
            // 先假设左边节点较大
            int max = left(x);
            // 如果右边节点存在，比一下大小
            if (right(x) <= size && less(max, right(x)))
                max = right(x);
            // 结点 x 比俩孩子都大，就不必下沉了
            if (less(max, x)) break;
            // 否则，不符合最大堆的结构，下沉 x 结点
            swap(x, max);
            x = max;
        }
    }

    /* 交换数组的两个元素 */
    private void swap(int i, int j) {...}

    /* pq[i] 是否比 pq[j] 小？ */
    private boolean less(int i, int j) {
        return pq[i].compareTo(pq[j]) < 0;
    }

    /* 还有 left, right, parent 三个方法
    分别表示节点的左儿子、右儿子、父亲 */
}

注意 js 除法不会自动取整

倒数第 k 个

  • 双指针
    • p1 走出 k 步之后, p1 和 p2 再同步移动

      只用遍历一次链表

链表-环

  • 双指针
    • p1 走一步,p2 走两步, while 循环
      • 如果 p2 === null, 说明没有环
      • 如果 p2 === p1 , 说明有环

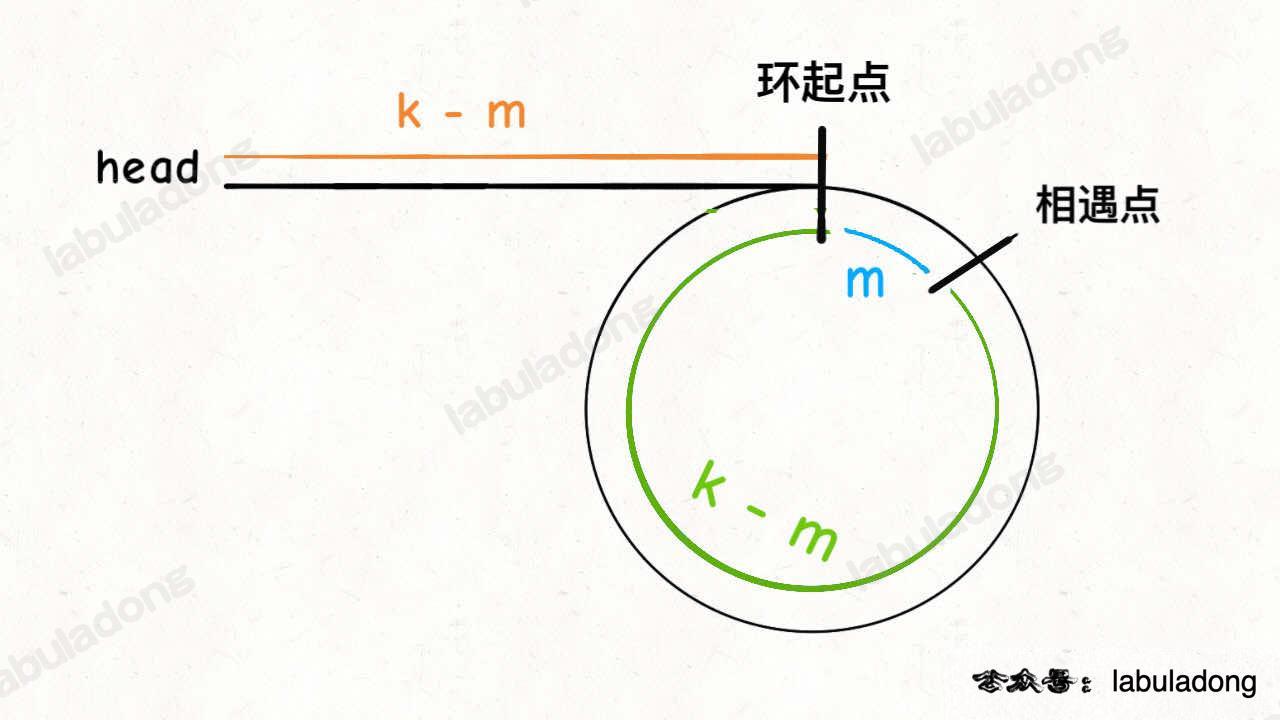
找到环的起点

  1. 使用上述双指针方法，知道快慢指针指向同一个位置。
  2. 再让一个指针回第一个节点，两个指针同步移动相同距离，
  3. 再次相遇位置即为环的起点

返回两链表相交点

p1 = [1,2,3,4]
p2 = [a,b,c,3,4]
则 3 是相交点
p1+p2 = [1,2,3,4,a,b,c,3,4]
p2+p1 = [a,b,c,3,4,1,2,3,4]

  • 拼接 p1+p2 和 p2+p1
    • 此时两个链表同步遍历下去, 若遇到两者相同的节点,则它就是相交点

数组

差分

  • 维护一个差分数组 diff[n] = arr[n] - arr[n-1]
  • 主要适用场景是频繁对原始数组的某个区间的元素进行增减 。

例如：在 [ i , j ] 之间 所有元素都加1
只需要 diff[ i ] += 1 ; diff[ j+1 ] -= 1;

遍历

  • 旋转矩阵
    • 沿着主对角线对折后，再rever每行元素 = 顺时针旋转90°
  • 螺旋遍历矩阵

    1. 用一个d 和 一个flag 辅助数组 遍历 ， 空间复杂度O(m*n)

      1
      2
      3
      4
      5
      6
      const d = {
          0: [0, 1],
          1: [1, 0],
          2: [0, -1],
          3: [-1, 0]
      }

    2. 空间复杂度O(1)

      1
      2
      var upper_bound = 0, lower_bound = m - 1;
      var left_bound = 0, right_bound = n - 1;

T54 T54

滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const window = new Map()
let left = 0, right = 0;
let valid = 0; //记录收集完成的字母的数量

while (left < right && right < s.length) {
    // 增大窗口
    window.set(s[right], window.get(s[right])?window.get(s[right])+1: 1);
    right++;
  
    while (window needs shrink) {
        // 缩小窗口
        window.set(s[left], window.get(s[left])-1);
        left++;
    }
}

二分搜索

  • 防止溢出 (l+r)/2 === l + (r - l)/2

左侧边界优先二分搜索

不同的二分搜索对于 [1,2,2,2,3] return 2 而不是 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function left_bound_binary_search (nums, target) {
    let left = 0, right = nums.length - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        let mid = left + ((right - left) >> 1);
	if (nums[mid] == target){
            // 收缩右侧边界 ⭐不return
            right = mid - 1;
	} else if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        }
    }
    // 判断 target 是否存在于 nums 中
    // 如果越界，target 肯定不存在，返回 -1
    if (left < 0 || left >= nums.length) {
        return -1;
    }
    // 判断一下 nums[left] 是不是 target
    return nums[left] == target ? left : -1;
};

右侧边界优先二分搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function right_bound_binary_search (nums, target) {
    let left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) >> 1;
	if (nums[mid] == target){
            //【区别1】
            left = mid + 1;
	} else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }
    // 【区别2】
    if (right < 0 || right >= nums.length) {
        return -1;
    }
    // 【区别3】
    return nums[right] == target ? right : -1;
};

树

二叉搜索树

  • 搜索
1
2
3
4
5
6
7
8
9
10
11
var BST = function(root, target) {
    if (root.val === target) {
        // 找到目标，做点什么
    }
    if (root.val < target) { 
        BST(root.right, target);
    }
    if (root.val > target) {
        BST(root.left, target);
    }
};
  • 插入
1
2
3
4
5
6
7
8
9
10
11
var insertIntoBST = function(root, val) {
    // 找到空位置插入新节点
    if (root === null) return new TreeNode(val);
    // if (root.val == val)
    //     BST 中一般不会插入已存在元素
    if (root.val < val) 
        root.right = insertIntoBST(root.right, val);
    if (root.val > val) 
        root.left = insertIntoBST(root.left, val);
    return root;
}
  • 删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * 删除 BST 中的一个节点并返回根节点。
 * @param {TreeNode} root - 二叉树的根节点。
 * @param {number} key - 待删除节点的值。
 * @return {TreeNode} - 删除节点后的 BST。
 */
var deleteNode = function(root, key) {
    if (root == null) return null;
    if (root.val == key) {
        // 这两个 if 把情况 1 和 2 都正确处理了
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        // 处理情况 3
        // 获得右子树最小的节点
        let minNode = getMin(root.right);
        // 删除右子树最小的节点
        root.right = deleteNode(root.right, minNode.val);
        // 用右子树最小的节点替换 root 节点
        minNode.left = root.left;
        minNode.right = root.right;
        root = minNode;
    } else if (root.val > key) {
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        root.right = deleteNode(root.right, key);
    }
    return root;
}

/**
 * 获得 BST 中最小的节点。
 * @param {TreeNode} node - 待查找 BST。
 * @return {TreeNode} - BST 中最小的节点。
 */
var getMin = function(node) {
    // BST 最左边的就是最小的
    while (node.left != null) node = node.left;
    return node;
}

图

dfs遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var visited = [];
var onPath = [];

/* 图遍历框架 */
function traverse(graph, s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (var i = 0; i < graph.neighbors(s).length; i++) {
        var neighbor = graph.neighbors(s)[i];
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

图的拓扑排序就是图的dfs后序排序再reverse

判断环

基于dfs，通过onPath.includes(cur)判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
var findOrder = function (numCourses, prerequisites) {
    const visited = new Array(numCourses).fill(false)
    const onPath = [];
    const graph = generateGraph(numCourses, prerequisites)
    let hasCircle = false;

    for (let i = 0; i < numCourses; i++) {
        dfs(i)
    }
 
    return hasCircle 

    function dfs(cur) {
        if (onPath.includes(cur))//判断是否有环
            hasCircle = true;
        if (visited[cur] || hasCircle) 
            return;
        visited[cur] = true;
        onPath.push(cur)
        let p = graph[cur].next;
        while (p) {
            dfs(p.val);
            p = p.next;
        }
        onPath.pop();
    }
};

基于拓扑排序 拓扑顺序count===num

拓扑排序

  • dfs后序遍历再翻转
  • 基于bfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 构建邻接表、入度数组
let indegree = new Array(numCourses).fill(0);
let graph = buildGraph2(numCourses, prerequisites, indegree);
// 初始化，入度为0直接加入队列中
let q = [];
for (let i = 0; i < numCourses; i++) {
    if (indegree[i] == 0) {
        q.push(i);

    }
}

// 开始执行 BFS 循环
while (q.length > 0) {
    // 弹出一个节点，代表遍历了一个节点。
    let cur = q.shift();
    let p = graph[cur].next;
    while (p) {
        indegree[p.val]--; 
        if (indegree[p.val] === 0) { //此节点入度为0，可以入队
            q.push(p.val)
        }
        p = p.next;
    }
}

拓扑排序与dfs区别：使用indegree[]而不是visited[]

背包

0-1背包

要么装进包里，要么不装，不能说切成两块装一半

1
2
3
4
5
6
7
8
9
10
11
12
// 对于前 i 个物品（从 1 开始计数），当前背包的容量为 w 时，这种情况下可以装下的最大价值是 dp[i][w]。
const dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0

for i in [1..N]:
    for w in [1..W]:
        dp[i][w] = max(
            把物品 i 装进背包,
            不把物品 i 装进背包
        )
return dp[N][W]

完全背包

一个物品可以装进无限次，也可以不装

处理循环数组

  1. 下标取余
  2. 复制一份再首尾连接起来

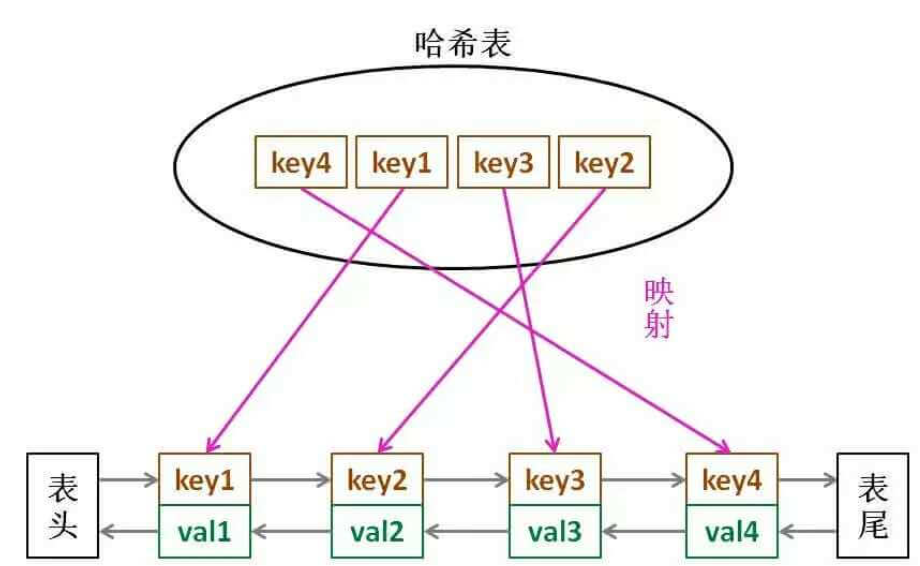
LRU

最近最旧未使用

LRU